Der Doppelspalt
Anwendung des huygensschen Prinzips auf den Doppelspalt
Nach dem huygensschen Prinzip stellen die zwei Spalte eines Doppelspalts jeweils eine Quelle für Elementarwellen dar.
Die beiden Elementarwellen breiten sich hinter dem Doppelspalt aus und überlagern sich dabei, es kommt zu konstruktiver und destruktiver Interferenz, wie folgende Animation zeigt (rote Linien stellen Wellenberge, blaue Linien Wellentäler dar).
An welchen Stellen sind diese Extrema?
Indem man einen Beobachtungsschirm hinter den Doppelspalt hält, kann leicht festgestellt werden, an welchen Stellen es zu maximal konstruktiver bzw. minimaler Interferenz kommt.
Diese Stellen können jedoch auch berechnet werden, man muss dabei zwei Fälle unterscheiden, einerseits die Fresnel'sche Betrachtungsweise und andererseits die Fraunhofer'sche Betrachtungsweise.
Die Fresnel'sche Betrachtungsweise verwendet man, wenn
- der Abstand b zwischen Doppelspalt (Spaltabstand g) und Schirm sehr klein ist,
- der Abstand zwischen Lichtquelle und Doppelspalt klein ist (in diesem Fall kann man nicht mehr sagen, dass eine ebene Wellenfront auf den Doppelspalt trifft),
- mathematisch formuliert: g2 ≥ λ⋅b
Die Fraunhofer'sche Betrachtungsweise verwendet man, wenn
- der Abstand b zwischen Doppelspalt (Spaltabstand g) und Schirm sehr groß ist,
- der Abstand zwischen Lichtquelle und Doppelspalt groß ist,
- mathematisch formuliert: g2 << λ⋅b
Im normalen Doppelspaltexperiment wählt man also die Fraunhofer'sche Betrachtungsweise, in diesem Fall ist das Muster leicht berechenbar.
Da der Abstand vom Schirm zum Gitter im Vergleich zum Spaltabstand sehr groß ist, können zwei sich überlagernde Wellenzüge als parallel zueinander betrachtet werden, wie es folgendes Schema zeigt.
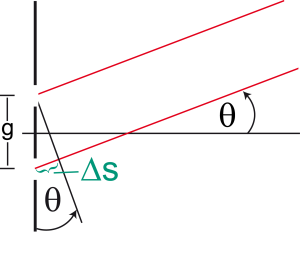
Der Gangunterschied Δs zwischen den beiden Wellenzügen ergibt sich aus folgender trigonometrischen Beziehung
Δs = g ⋅ sin θ
Für maximale Verstärkung muss dieser Gangunterschied gerade ein Vielfaches der Wellenlänge sein, da dann der Phasenunterschied zwischen den zwei Wellen gerade 0° (oder 360°) ist, man findet also dann ein Maxima, wenn gilt:
Maxima: Δs = g ⋅ sin θm = m ⋅ λ mit m=0,1,2,...
Entsprechend findet man Minima, wenn ein Wellenberg auf ein Wellental trifft (der Phasenunterschied ist dann gerade 180°), also
Minima: Δs = g ⋅ sin θm = (2m+1) ⋅ λ/2 mit m=0,1,2,...
Auf dem Schirm findet man demnach im Abstand dm zum Schirmmittelpunkt Extrema
dm = b⋅ tan θm
Da der Winkel θ klein ist, gilt die Näherung tan θ = θ, d.h. die Maxima sind äquidistant.
Mit einer genaueren Betrachtung kann die exakte Intensitätsverteilung hergeleitet werden:
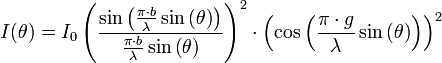
Oder graphisch aufgetragen:
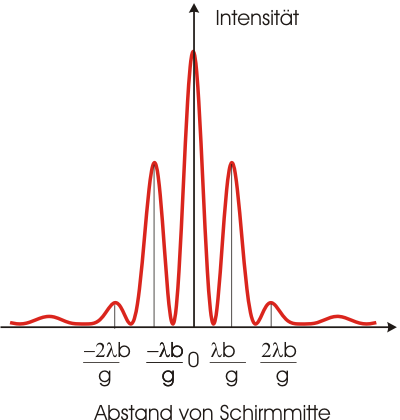
Man erkennt, dass die Lage der Maxima wellenlängenabhängig ist, d.h. der Doppelspalt ist auch eine "Art dispersives Element",
Am Dreifachspalt wird nun untersucht, welche Vorteile ein Gitter als dispersives Element statt eines Doppelspalts bringt.
Weiter zur Betrachtung des Dreifachspalts.
