zirkulare Polarisation

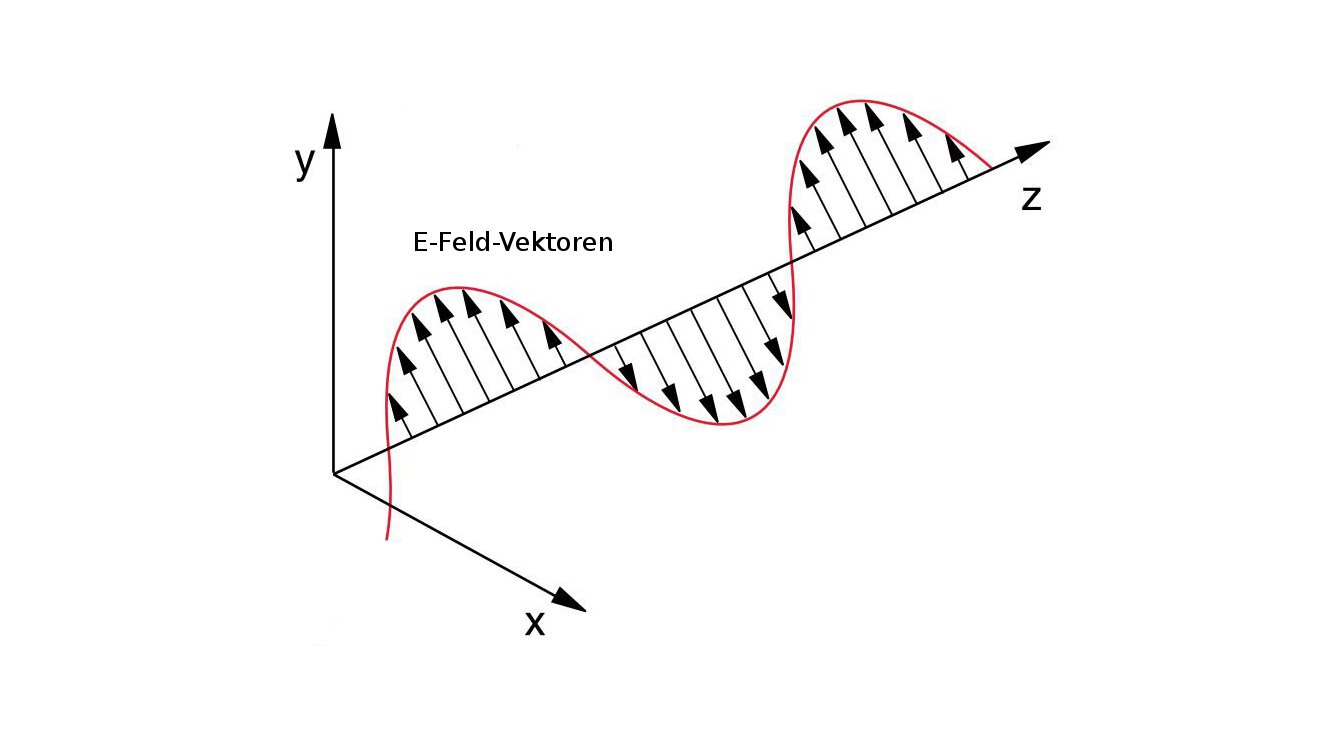
Die Polarisation einer transversalen Welle, also in diesem Fall einer Lichtwelle ist einfach gesagt nichts anderes als ihre Schwingungsrichtung. Eine transversale Welle schwingt senkrecht zu Ihrer Ausbreitungsrichtung (das heißt: der Vektor ihres elektrischen und auch magnetischen Feldes schwingt). Bei unpolarisierten Wellen findet man alle möglichen Schwingungsrichtungen, bei einer linear polarisierten Welle hat man beispielsweise nur eine bestimmte Schwingungsrichtung in einem bestimmten Winkel, wie Abb. 1 vereinfacht zeigt:

Abb. 1: Lineare Polarisation: Die Feldvektoren (hier eingezeichnet das elektrische Feld)
an verschiedenen Orten schwingen alle in derselben Richtung

In der Abbildung erkennt man, dass die E-Feldvektoren an jedem Ort der Welle in der gleichen Ebene/Richtung schwingen. Man erreicht das, in dem man z.B. unpolarisiertes Licht von einer Glühlampe durch einen Polarisationsfilter schickt, der in die gewünschte Richtung eingestellt ist. Hier wird auch schnell anschaulich: Möchte man derart polarisiertes Licht blockieren, so setzt man einfach einen weiteren Polarisationsfilter in den Strahl, der im 90°-Winkel, also senkrecht, zum vorherigen Filter orientiert ist. Da es senkrecht zur Polarisationsrichtung keine E-Feldkomponente gibt, wird das Licht nach dem 90°-Polarisator (oft auch Analysator) genannt, komplett ausgelöscht.

Was muss man sich aber nun unter zirkularer Polarisation vorstellen? Analog ist das im Grunde einfach: Betrachtet man den E-Feldvektor, so dreht er sich mit konstanter Winkelgeschwindigkeit und beschreibt mit fortlaufender Welle in der Transversalebene betrachtet einen Kreis. In Abb. 2 sieht man, dass die Welle rechts von dem runden Plättchen zirkular polarisiert ist - sie sieht schraubenartig aus.

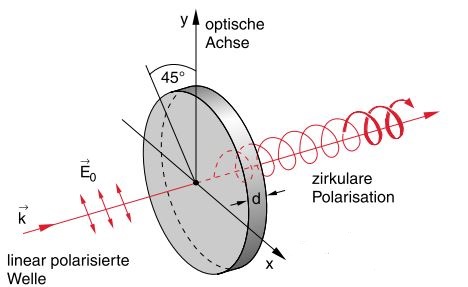
Abb. 2: Erzeugung zirkularer Polarisation¹

Doch wie erhält man zirkulare Polarisation? Man benötigt dazu im Grunde zwei optische Bauteile: einen linearen Polarisationsfilter und ein sogenanntes Verzögerungsplättchen oder Lambda/4-Plättchen. Denn trifft, wie in Abb. 2, linear polarisiertes Licht auf das Verzögerungsplättchen im 45°-Winkel zu dessen optischer Achse, so wird der E-Feldvektor in eine gleich große senkrechte und waagrechte Komponente aufgeteilt. Innerhalb des Plättchens der Dicke d ist aber die Ausbreitungsgeschwindigkeit des Lichts unterschiedlich, sodass sich am Ende zwischen den Feldkomponenten eine Phasenverzögerung einer viertel Wellenlänge ergibt (daher der Name Lambda/4-Plättchen). Durch diese Phasenverschiebung beschreibt der E-Feldvektor der Lichtwelle nach Austritt aus dem Plättchen einen Kreis. Je nachdem, nach welcher Seite von der optischen Achse des Verzögerungsplättchens die lineare Polarisation um 45° geneigt ist, erhält man rechts- oder linkszirkular polarisiertes Licht. In Abb. 2 dreht der E-Vektor gegen Uhrzeigersinn, wenn man die Welle auf sich zukommen sieht. Daher spricht man von linkszirkularer Polarisation. Bei Drehung im Uhrzeigersinn erhält man rechtszirkular polarisiertes Licht.

Möchte man also aus völlig unpolarisiertem Licht, das z.B. aus einer Glühlampe kommt, zirkular polarisiertes Licht machen, so muss man das Licht zunächst durch einen linearen Polarisationsfilter und anschließend durch ein Verzögerungsplättchen schicken. Der lineare Polarisator muss im 45°-Winkel zur optischen Achse des Verzögerungsplättchens stehen.

Da für die 3D-Kinotechnik die zirkulare Polarisation genutzt wird, ist die Kinobrille entsprechend aufgebaut wie in Abb. 3 skizziert. Auf der zum Auge gerichteten Seite befindet sich der lineare Polarisationsfilter, auf der zur Leinwand gerichteten Seite das Verzögerungsplättchen. Die linearen Polarisationsfilter beider Brillengläser sind parallel ausgerichtet, während die Verzögerungsplättchen so eingestellt sind, dass auf einem Auge linkszirkularpolarisiertes Licht durchgelassen wird und auf dem anderen rechtszirkular polarisiertes, denn:

Ein Filtersystem, das linkszirkular polarisiertes Licht durchlässt, sperrt rechtszirkular polarisiertes und umgekehrt.

Abb. 3: Aufbau der Kinobrille