Michelson-Interferometer

Das Michelson Interferometer is benannt nach dem Physiker Albert Abraham Michelson, der 1907 für seine Arbeiten daran den Nobelpreis erhielt. Es ist besonders bekannt aus dem Michelson-Morley Experiment, dem berühmtesten Negativ-Experiment der Physik, welches den Äther beweisen sollte, sowie seit Neuestem für die Detektion von Gravitationswellen. Daneben wird es häufig in optischen Messinstrumenten verwendet, wie zum Beispiel bei der optischen Kohärenztomographie. 

Aufbau des Michelson Interferometers

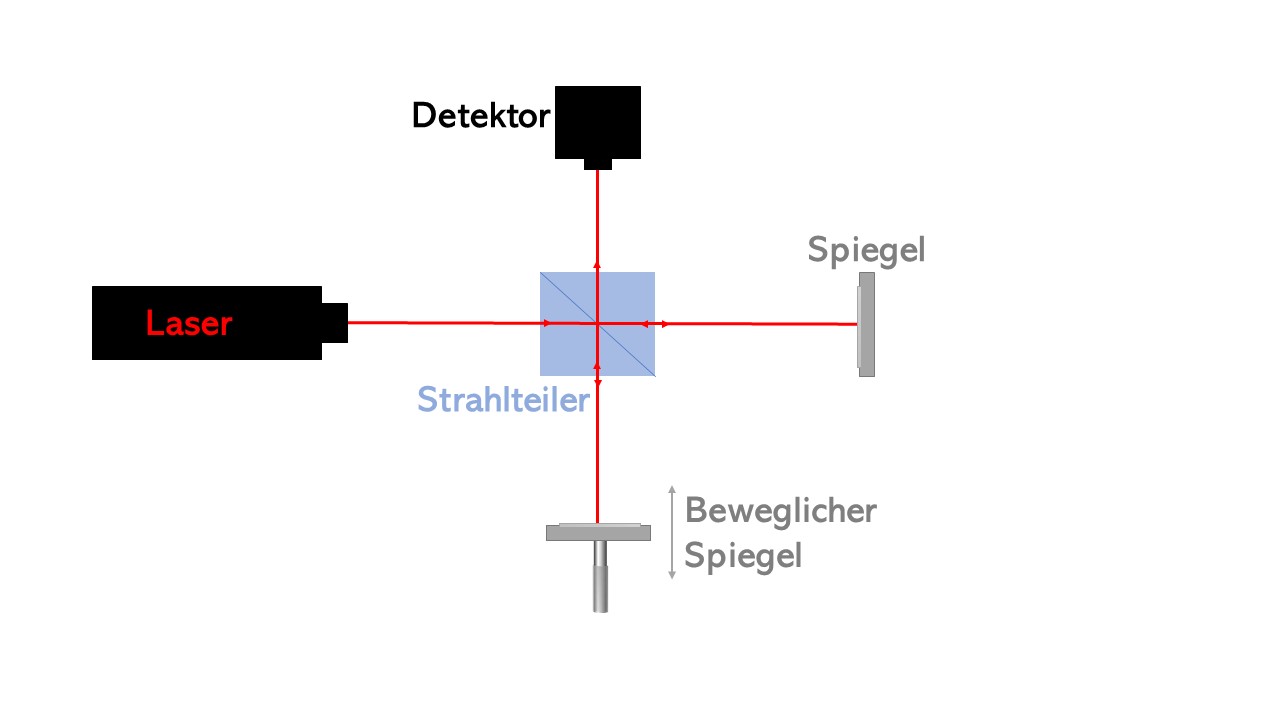
In Abbildung 1 ist der gesamte Aufbau eines Michelson Interferometers mit Detektor abgebildet. Um den Aufbau des Michelson Interferometers zu verstehen, müssen zuerst die Eigenschaften der einzelnen Bauteile verstanden werden. Falls diese alle bekannt sind, kann zur Funktionsweise gesprungen werden.

• Die Spiegel: Aus unserem alltäglichen Leben bekannt: Die Spiegel reflektieren das eintreffende Licht wieder zurück. Besonders ist nun: einer der beiden Spiegel ist je nach Experiment beweglich. Oft ist dies ganz einfach: an einer Schraube drehen und der Spiegel bewegt sich.
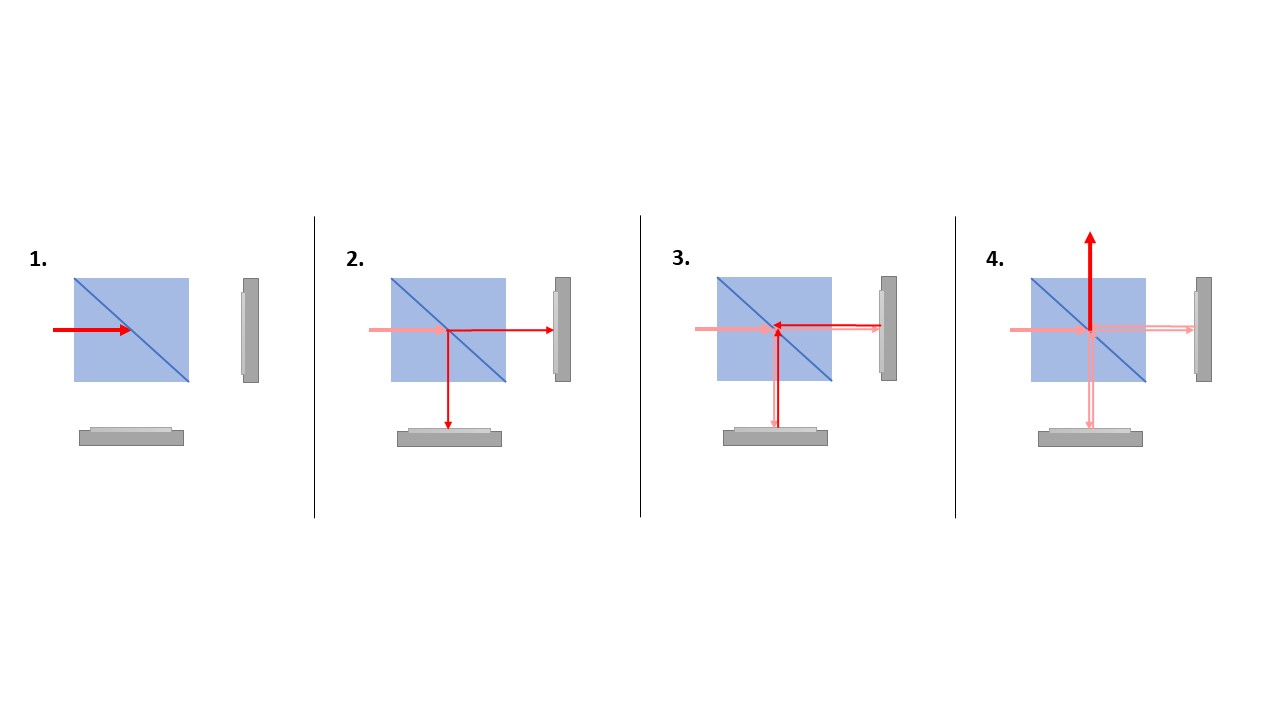
• Der Strahlteilerwürfel: Der zentrale Baustein des des Michelson Interferometers ist der Strahlteiler. Oft wird an dieser Stelle ein sogenannter Strahlteilerwürfel verwendet. Ein solcher Strahlteilerwürfel besteht aus zwei aneinandergeklebten rechtwinkligen Prismen. Die Klebefläche reflektiert einen Teil des eintreffenden Lichts und lässt den Rest gerade durch. (Oft wird hier ein sogenannter 50:50 Strahlteiler verwendet. Das bedeutet, dass 50% des Lichts reflektiert werden und 50% geradeaus weiterläuft.) Abbildung 2 zeigt den Strahlengang bei der Verwendung eines solchen Strahlteilerwürfels im Michelson Interferometer. Die beiden reflektierten Strahlen werden dann auf dem Rückweg miteinander überlagert, sie interferieren also miteinander. Wenn das Licht von den Spiegeln zurückreflektiert wird, passiert es den Strahlteiler noch einmal. Auch auf diesem Weg werden jeweils wieder 50% reflektiert und 50% laufen weiter. In der Skizze sind von diesen Wegen nur diejenigen eingezeichnet, welche im Detektor landen. Dies dient rein der Vereinfachung.

• Der Laser: Laser erzeugen im Idealfall Licht mit nur einer einzigen Wellenlänge. Die Lichtstrahlen verlaufen parallel, wir können mit den besten Lasern also einen Punkt auf den Mond leuchten, was wir mit unserer Taschenlampe leider nicht hinbekommen. In dem Experiment bedeutet das, dass das Licht immer ungefähr gleich "breit" ist und immer ungefähr die gleiche Wellenlänge hat. In der Fachsprache spricht man oft davon, dass Laserlicht kohärent ist. Kohärenz ist kein einfaches Thema, aber falls du mehr dazu lesen/hören möchtest, dann kannst gerne hier mehr nachlesen.   
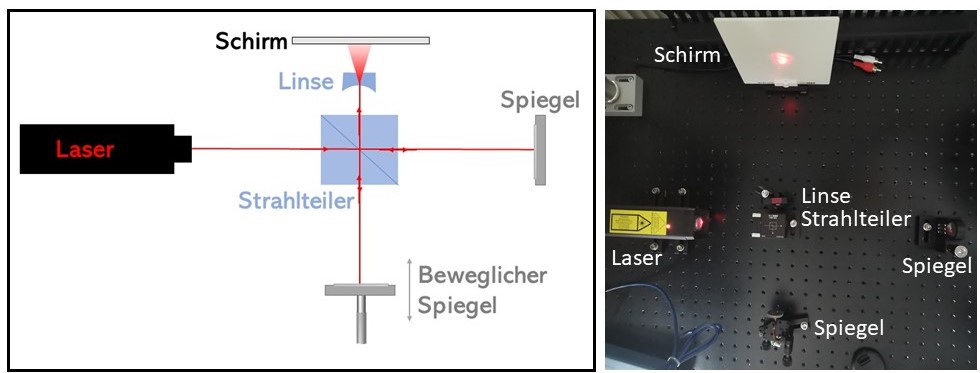
• Der Detektor: In modernen Experimenten können hier Kameras verwendet werden. Eine bekannte Alternative ist die Verwendung einer Aufweitungslinse und eines Schirms, wie in Abbildung 3 dargestellt. Die Aufweitungslinse ist nötig, da unser Auge sonst nicht in der Lage ist, Veränderungen des Laserstrahls zu erkennen. (Wenn unsere Strahlen interferieren, so würde ohne Linse der Laserpunkt auf dem Schirm zwischen hell und dunkel flackern, weiten wir den Strahl mithilfe der Linse, so beleuchten wir nicht nur einen kleinen Punkt, sondern einen größeren Bereich. Nun entstehen allerdings Interferenzringe (Abbildung 4), da die Lichtstrahlen unterschiedlich lange Wege zurücklegen.)

Funktionsweise des Michelson Interferometers

Das Michelson-Interferometer misst den Längenunterschied der Abstände zwischen den jeweiligen Spiegeln und dem Strahlteiler durch Interferenz. Haben die beiden Spiegel den gleichen Abstand zum Strahlteiler, so legt das Licht auf beiden Wegen die gleiche Strecke zurück, wir haben also keinen Phasenunterschied und die beiden Strahlen interferieren konstruktiv. Das bedeutet, unser Detektor detektiert ein sehr helles Licht. Drehen wir nun an der Schraube und verschieben einen Spiegel, so muss ein Lichtstrahl einen längeren (oder kürzeren) Weg zurücklegen. Wir erzeugen also einen Gangunterschied und die beiden Strahlen interferieren nun nicht mehr konstruktiv. Hierdurch wird unser Lichtpunkt im Detektor dunkler, bis wir einen Phasenunterschied von  erreichen: nun löschen sich die beiden Strahlen komplett aus, der Lichtpunkt ist komplett dunkel. Drehen wir weiter an der Schraube wird der Lichtpunkt zuerst wieder heller, bis er maximal hell ist, und dann wieder dunkler. Das ganze beginnt Dank der Periodizität von Lichtwellen also wieder von vorne.

Durch diese Periodizität  können wir mit einem Michelson-Interferometer auch nie messen, wie lange die beiden Lichtwege sind, sondern nur, wie die Wege sich im Verhältnis zueinander verändern. Wenn wir aber einen Spiegel stabil befestigen, so können wir mit dieser Methode dennoch sehr, sehr genau messen und so zum Beispiel Gravitationswellen detektieren.

Etwas mathematischere Beschreibung

Wir benennen: 

• s₁: Länge von Strahlengang 1
• s₂: Länge von Strahlengang 2
• Δs = |s₁ - s₂|: sogenannte Gangdifferenz (der Längenunterschied der beiden Strahlengänge)
• d: Länge um welche wir den verstellbaren Spiegel verstellt haben, wenn zuvor beide Spiegel den gleichen Abstand zum Strahlteilerwürfel hatten

Und können nun bereits feststellen: 

• Verstellen wir den Spiegel z.B. um d = 2cm nach hinten, so muss das Licht in Strahlengang 2 ganze 4cm mehr zurücklegen, da es durch die Reflektion die Strecke doppelt durchläuft. Wir haben damit als Gangdifferenz Δs = 4cm. Bzw allgemein gesagt gilt: Δs = 2d.

Wir können Licht als elektromagnetische Welle beschreiben. Meist verwendet man hierfür die Beschreibung als homogene ebene Welle. Das ist praktisch, denn diese Beschreibung ist sehr ähnlich zu denen,  die du bestimmt bei klassischen Wellen schon in der Schule verwendet hast. 
Das elektrische Feld E unseres Lichts können wir somit als ebene Welle ausdrücken als:

E(t,x) = A^.sin(ωt - kx + φ)

wobei wir verwenden

• A: Die Amplitude unseres Lichts
• ω: Die Kreisfrequenz unseres Lichts, welche mit der Wellenlänge des Lichts zusammenhängt durch ω = 2πc/λ (c: Lichtgeschwindigkeit)
• k: die sogenannte Wellenzahl, welche (in den Medien, welche wir betrachten) ist: k = 2π/λ
• x: der Ort, welchen wir betrachten
• φ: zusätzliche Phase.

Wenn wir nun zwei Wege haben, welche das Licht gehen kann, so haben wir am Ende zwei ebene Wellen miteinander interferieren. Diese beiden Wellen lassen an einem Ort x₀ (z.B. dem Detektor) zu einer Zeit t₀ mithilfe einer Konstanten C beschreiben als:

E₁ = A^.sin(C) und E₂ = A^.sin(C + φ)

wobei wir nutzen, dass unsere beiden Wellen ursprünglich aus der gleichen Quelle kommen, also die gleiche Wellenlänge und - wenn wir einen perfekten  50:50 Strahlteiler verwenden - die gleiche Amplitude haben. Unsere zusätzliche Phase φ ist somit rein durch die Gangdifferenz entstanden und wir können diese Phase bestimmen durch

φ = k ^. Δs = 2π/λ ^. Δs .

Wir sehen somit: 

• Ist Δs = λ, dann ist φ = 2π und da der Sinus periodisch mit 2π ist (d.h.: A^.sin(C + 2π) = A^.sin(C) ) gilt: E₁ = E₂ und wir haben perfekt überlagernde Wellen, also konstruktive Interferenz.
• Ist Δs = λ/2, dann ist φ = π und da gilt A^.sin(C + π) = - A^.sin(C) ) gilt: E₁ = - E₂ und unsere überlagernden Wellen löschen sich komplett aus, also destruktive Interferenz.
• Im Allgemeinen können wir die Intensität der interferierenden Wellen berechnen über: I = |E₁ + E₂|².

Durch diesen direkten Zusammenhang können wir aus der Intensität am Detektor zurückschließen auf den Gangunterschied Δs. Wir merken aber auch, dass es keinen Unterschied macht, ob wir Δs = λ oder Δs = 15λ als Gangunterschied haben. Diesen letzten Punkt müssen wir beim Michelson Interferometer immer bedenken.