Der Eigenbau-Quantenzufallsgenerator
Aus der Quantemechanik wissen wir, dass die Wellenfunktion eines quantenmechanischen Objekts, wie z.B. eines Photons oder Elektrons, dessen Zustand beschreibt (z.B. Ort, Impuls,...). Mittels des Betragsquadrats dieser Wellenfunktion können Aussagen über die Aufenthaltswahrscheinlichkeit der entsprechenden Objekte beispielsweise beim Durchgang durch einen Doppelspalt getätigt werden (siehe dazu auch den Versuch „Quantenradierer“). Wie “entscheidet” aber das einzelne Photon oder Elektron, welchen Weg es wählt? Dieser Prozess ist, genau wie beispielsweise der Zerfall eines einzelnen radioaktiven Kerns, völlig zufällig.
Die Frage ist nun – kann man diesen Zufall messen? Man kann!
Der experimentelle Aufbau, wie wir ihn im Schülerlabor realisiert haben, ist in der folgenden Abbildung zu sehen:

Aufbau eines Experiments zur Aufnahme von Zufallszahlen
Es wird ein durch einen Absorber stark abgeschwächter Laserstrahl auf einen Strahlteiler gerichtet. Zwei Einzelphotondetektoren sind so angeordnet, dass einer den reflektierten Anteil (wir bezeichnen diese Ereignisse mit “0”) und einer den transmittierten Anteil des Strahls (“1”) misst. Im Mittel werden bei richtiger Justage jeweils 50% der Photonen pro Detektor eintreffen – die Frage ist aber: An welchem Detektor wird das einzelne Photon detektiert?
Mit Hilfe eines Oszilloskops werden nun die Signale beider Detektoren überlagert – damit wissen wir, wann bei welchem Detektor ein Photon eingetroffen ist. Nun kodieren wir das Messergebnis: Für jedes Photon, das beim ersten Detektor eintrifft, schreiben wir eine 1, für jedes Photon am Detektor zwei schreiben wir eine 0 (wie oben schon angesprochen) – natürlich in der Reihenfolge, wie sie beim jeweiligen Detektor eingetroffen sind. Außerdem muss unbedingt gewährleistet sein, dass die Wahrscheinlichkeit für das Auftreffen eines Photons auf einem Detektor wirklich jeweils 50% ist.
In einer Momentaufnahme des Oszilloskop-Schirms sieht das folgendermaßen aus:
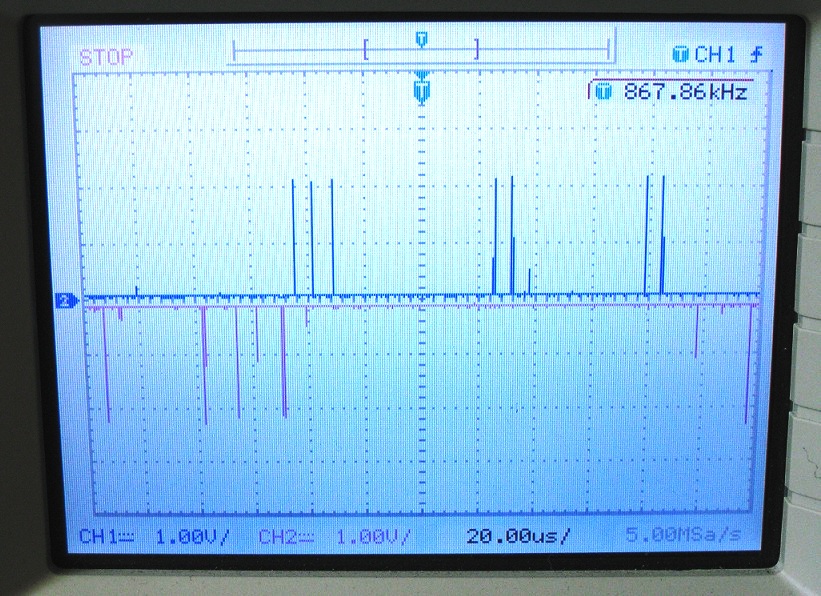
Momentaufnahme im Ozilloskopbild der an 2 Detektoren ankommenden Photonen
Jeder Peak, der nach unten zeigt, repräsentiert ein Photon, das am Strahlteiler reflektiert wurde und somit von unserem Detektor registriert wird, dessen Ereignisse wir “0” nennen. Die nach oben gerichteten Peaks stammen von am Strahlteiler transmittierten Photonen, die am Detektor „1“ angekommen sind (Wir zählen dabei nur Peaks mit voller Höhe (2V, also 2 Kästchen)).
Daraus ergibt sich eine Zahlenfolge, die in unserem speziellen Fall oben nun so aussieht:
0 0 0 0 1 1 1 1 1 1 1 0
Woher wissen wir nun aber, ob diese Reihenfolge wirklich zufällig ist? Das beantworten wir damit, dass wir uns überlegen, wie eine Zufallszahlenfolge aussehen würde, wenn wir sie mit einer Münze erstellen würden. Die Wahrscheinlichkeit, dass man mit einer Münze z.B. 3 mal hintereinander Kopf wirft (das nennen wir dann einfach '1'), liegt bei 1/8 (also ½ hoch 3). Wir wissen also, dass die Häufigkeit einer Kette exponentiell mit ihrer Länge abnehmen sollte – also eine Kette 01110 doppelt so wahrscheinlich ist, wie die Kette 011110. Jetzt zählen wir in der gemessenen Zahlenfolge ab, wieviele 1er-Ketten da sind und wie lang sie sind. Das vergleichen wir dann mit dem theoretisch erwarteten exponentiellen Abfall – und finden tatsächlich, dass der Durchgang der einzelnen Photonen durch den Strahlteiler komplett zufällig erfolgt! Das werden wir im nächsten Kapitel gleich in der Auswertung sehen.
Um statistisch aussagekräftige Zufallsfolgen zu erhalten, müsste man sehr lange eine Münze werfen oder obige Quantenmessung mit dem Oszilloskop sehr häufig durchführen, was äußerst zeitaufwendig wäre.
Bemerkenswerterweise sind heute bereits Geräte auf dem Markt, die ähnlich zu unserem Experiment quantenphysikalische Zufallszahlen liefern und dabei auch noch unglaublich kompakt und leicht zu bedienen sind. Lesen Sie dazu sowie zu einer einfachen Veranschaulichung des Zufalls aufgrund der gewonnenen Daten mehr im Kapitel "Quantenzufall aus der Hosentasche".
