Das optische Gitter

Nun sollen die beim Übergang vom Doppel- zum Dreifachspalt gewonnenen Erkenntnisse auf N Spalte verallgemeinert werden. 
Anhand der folgenden  Intensitätsverteilungen der Mehrfachspalte mit N=3, 4 und 5 werden nun allgemeine Aussagen über optische Gitter anschaulich gemacht.

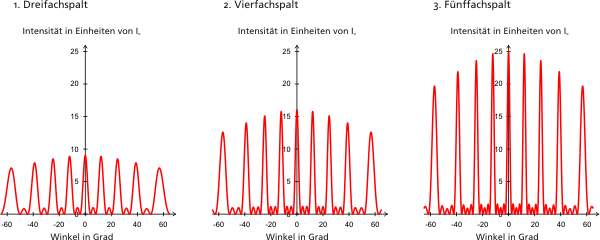
skalierbare Vektorgraphik dieses Schaubilds

Aussage 1

Das Interferenzmuster von Gittern ist viel heller als das von einem Doppelspalt, weil sich mehr Strahlen überlagern können.
Wenn A₀ die Amplitude eines Strahls von einem Spalt ist, so ist die Intensität des 0. Hauptmaximums eines Gitters mit N Spalten

I(θ=0) = N² ⋅ I₀

Aussage 2

Damit alle N Strahlen maximal konstruktiv interferieren können, muss der relative Gangunterschied zwischen ihnen jeweils ein Vielfaches der Wellenlänge sein, diese Helligkeitsmaxima sind unter den Winkeln θ_m zu finden, diese sind durch die Gittergleichung gegeben

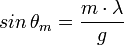
Aussage 3

Zwischen den  Hauptmaxima liegen N-2 Nebenmaxima mit einer sehr viel geringeren Intensität.

Aussage 4

Zwischen zwei Hauptmaxima liegen N-1 Minima, das erste Minimum liegt also sehr nahe am jeweiligen Hauptmaximum, damit ist dieses sehr scharf.

Zur Erläuterung betrachten wir ein Gitter mit N=100 Spalten.
Das Maximum k-ter Ordnung liegt dann vor, wenn der Gangunterschied

Δs = m ⋅ λ

beträgt.
Direkt daneben, bei einem Gangunterschied von  

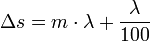
löschen sich alle Strahlen aus: und zwar die vom 1. und 51., die vom 2. und 52., …, die vom 50. und 100. Spalt.
In einer Formel verallgemeinert: Das erste Minimum nach einem Maximum k-ter Ordnung ist dort zu finden, wo der Gangunterschied

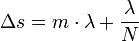
beträgt.