Der Dreifachspalt
Nach der Betrachtung des Doppelspalts wird nun gezeigt, wie sich eine Erhöhung der Anzahl von Spalten auswirkt.
Dazu wird zunächst der Dreifachspalt untersucht und dabei die Verwendung von Zeigerdiagrammen eingeführt, die gewonnen Erkenntnisse können anschließend leicht auf einen Mehrfachspalt mit N Spalten verallgemeinert werden.
Damit kann verstanden werden, was das besondere an einem Gitter, also einem Mehrfachspalt mit einer sehr großen Anzahl an Spalten, ist.
Beim Doppelspalt interferierten die zwei Wellenzüge genau dann maximal, wenn der Phasenunterschied gerade 0° war, oder anders ausgedrückt, an Orten, wo der Gangunterschied zwischen den beiden Wellen gerade ein Vielfaches der Wellenlänge war.
Beim Dreifachspalt ist das genau so: Um maximale Interferenz zu beobachten, muss die Phasendifferenz zwischen dem ersten und zweiten sowie dem zweiten und dritten Strahl 0 sein, der Dreifachspalt hat seine Maxima an der selben Stelle, allerdings haben sie eine höhere Intensität, da an diesen Stellen ja drei (statt zwei beim Doppelspalt) Wellenzüge interferieren.
Dies soll auch noch mit Hilfe von Zeigern (siehe Zeigerdiagramme) dargestellt werden:
Die roten Zeiger stellen die Ausgangsamplitude (des elektrischen Feldes) dar, sie werden dem Phasenwinkel entsprechend aneinander gelegt, durch Vektoraddition erhält man die resultierende Amplitude (in grün dargestellt).
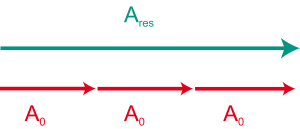
Die Intensität ist gerade das Quadrat der Amplitude, d.h. die relative Intensität beim Dreifachspalt ist
I = (Ares)2 = (3A0)2 = 9 (A0)2
Im Vergleich hierzu ist die relative Intensität beim Doppelspalt
I = (Ares)2 = (2A0)2 = 4 (A0)2
Zurück zum Dreifachspalt: Was passiert, wenn die Phasendifferenz zwischen jeweils Wellenzügen nicht gerade 0 ist, d.h. der Gangunterschied nicht ein Vielfaches der Wellenlänge ist?
Untersuchen wir mit Hilfe der Zeigerdigramme für verschiedene Phasendifferenzen, wie groß die resultierende Amplitude ist.
1. Relative Phasendifferenz Δφ = π
Die Zeiger müssen im Winkel von 180° aneinander gelegt werden, also:
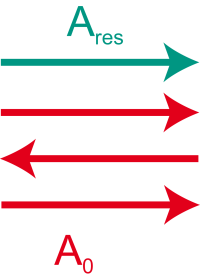
Die Zeiger löschen sich nicht ganz aus, d.h. an diese Stelle fällt Licht. Variieren wir die Phasendifferenz minimal nach oben oder nach unten, wird Ares kleiner, bei Δφ = π ist also ein so genanntes Nebenmaximum, dieses hat aber nur 1/9 der relativen Intensität im Vergleich zum Hauptmaximum.
Zwischen zwei Maxima muss sich ein Minimum befinden, wo ist dieses? Versuchen wir es mit Δφ = 1/3π
2. Relative Phasendifferenz Δφ = 1/3π
Die Zeiger müssen im Winkel von 60° aneinander gelegt werden, also
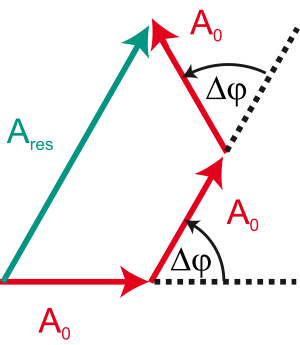
Wir erhalten eine resultierende Amplitude, die zwischen der von Haupt- bzw. Nebenmaxima liegt. Probieren wir als nächstes Δφ = 2/3π.
3. Relative Phasendifferenz Δφ = 2/3π
Die Zeiger müssen im Winkel von 120° aneinander gelegt werden, also
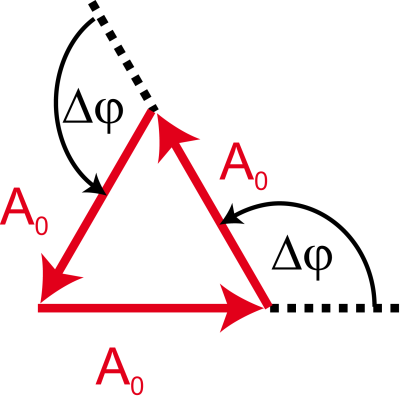
Wir drehen uns im Kreis – oder anders ausgedrückt, die resultierende Amplitude ist 0, d.h. wir haben ein Minimum gefunden.
Wo ist dieses Minimum auf dem Schirm zu finden?
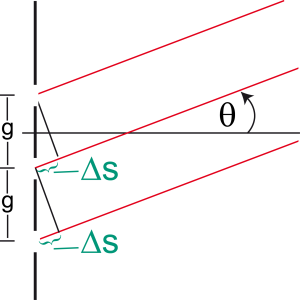
Die Lage des Minimums auf dem Schirm kann leicht aus dem Gangunterschied und damit aus der Phasendifferenz ermittelt werden.
Wir wissen, dass gilt
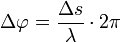
und
Δs = g ⋅ sin θ
Die Lage dieses Minimums berechnet sich also zu
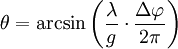
Vergleichen wir nun die Lage des ersten Minimums beim Dreifachspalt mit dem des Doppelspalts.
Wir nehmen dazu an, dass sowohl ein Doppel- und Dreifachspalt mit rotem Laserlicht der Wellenlänge 600 nm beleuchtet wird und weiterhin, dass der Spaltabstand bei Doppel- und Dreifachspalt der gleiche ist, nämlich 3 mal 10-4 m.
Für den Dreifachspalt war das erste Minimum bei Δφ = 2/3π, also
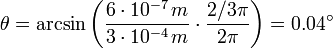
Für den Doppelspalt war das erste Minimum bei Δφ = π, also
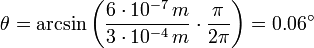
Beim Dreifachspalt liegt das erste Minimum also näher bei Hauptmaximum, d.h. das Hauptmaximum erscheint schärfer.
Dies ist auch deutlich an der berechneten Intensitätsverteilung zu erkennen:
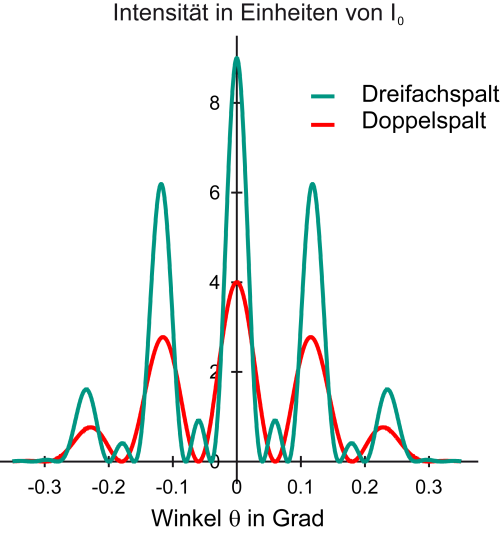
Man erkennt folgendes:
- die Lage der Hauptmaxima ist beim Doppel- und Dreifachspalt die selbe,
- die Intensität beim Dreifachspalt ist höher, da ja drei Strahlen interferieren,
- beim Dreifachspalt liegt zwischen dem 0. Hauptmaximum und dem ersten Hauptmaximum ein Nebenmaximum, dadurch rückt auch das erste Minimum näher an das 0. Hauptmaximum, dieses ist daher schärfer.
Weiter zum optischen Gitter, hier werden die oben gewonnenen Erkenntnisse auf einen Mehrfachspalt mit N Spalten, Gitter genannt, erweitert.
