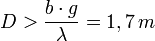Das historische Doppelspaltexperiment
Heute wird das Doppelspaltexperiment fast immer mit LASERn als Lichtquelle durchgeführt, da kohärentes Licht Voraussetzung für Interferenz ist.
Das Doppelspaltexperiment wurde jedoch bereits um 1800 von dem britischen Arzt und Physiker Thomas Young durchgeführt – also lange vor der Erfindung des Lasers, wie also konnte Young überhaupt Interferenzen erhalten?
Im Alltag kennen wir zwar Interferenzeffekte, diese rühren aber meist von dünnen Schichten her, z.B. das farbige Schimmern einer Seifenblase.
Halten wir jedoch z.B. zwei Taschenlampen nebeneinander, so sehen wir keine Interferenzeffekte.
Young verwendete für seinen Versuch Sonnenlicht, also unkohärentes Licht. Lassen wir den Experimentator selbst seinen Aufbau beschreiben:
| "Ich machte ein kleines Loch in einen Fensterladen, überdeckte es mit einem Stück dicken Papieres, in das ich mit einer feinen Nadel ein Loch stach, und benutze einen Spiegel, um den dünnen Lichtstrahl umzuleiten, der durch das Loch kam. Ich nahm die dünne, ungefähr ein dreißigstel Inch (Anmerkung: etwa 0,85 mm) breite Seite einer Spielkarte und hielt sie in den Weg des Lichtstrahls, sodass dieser zweigeteilt wurde. Ich beobachtete den Schatten: neben farbigen Streifen zu beiden Seiten des Schattens war der Schatten selbst durch ähnliche parallele Streifen geteilt." aus: T. Young 1804 Experiments and calculations relative to physical optics (The 1803 Bakerian Lecture) Philosophical Transactions of the Royal Society of London 94 1-16 |
Das Geheimnis liegt in dem kleinen Loch im Fensterladen, dieses stellt einen Kohärenzspalt dar.
Die Sonne ist eine ausgedehnte Lichtquelle, die darin enthaltenen Atome strahlen vollkommen unabhängig voneinander Licht ab, das Sonnenlicht ist also nicht kohärent.
Durch den Spalt muss das Licht also zumindest partiell kohärent gemacht worden sein, nur so können hinter dem Doppelspalt Interferenzmuster entstehen.
Wie funktioniert das?
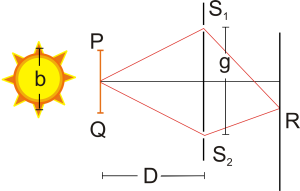
Die Lichtquelle hat eine Ausdehnung der Breite b, die äußersten Punkte sind P und Q. Jeder Punkt zwischen diesen beiden emittiert auch Licht, die Überlagerung aller Teilwellen ergibt die Gesamtamplitude und Phase der Welle in einem beliebigen Punkt, also auch an den Spalten S1 und S2.
Da die Lichtquelle nicht kohärent ist, wird die Gesamtphase in S1 bzw. S2 statistisch schwanken. Falls diese Schwankungen in S1 und S2 synchron verlaufen, beobachtet man auf dem Schirm dennoch ein Interferenzmuster, da einzig die Phasendifferenz der von S1 und S2 ausgehenden Wellen relevant ist.
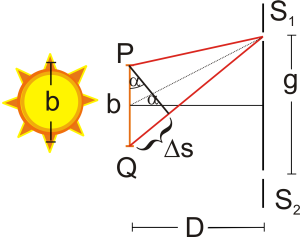
Diese Bedingung ist für Licht, das in der Mitte der Lichtquelle erzeugt wird gegeben, nicht aber für alle andere Punkte. Betrachtet man einen Spalt, so muss das Licht je nach dem Ort der Emission verschieden lange Wege zurücklegen, diese Wegdifferenz sei Δs.
Um Interferenz beobachten zu können, muss diese Wegdifferenz kleiner als λ/2 sein.
Betrachtet man die Geometrie der Anordnung, so gilt:
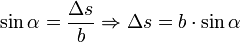
und
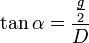
Für einen kleinen Winkel α (d.h. D >> g) gilt sin(α) ≈ tan(α) und somit
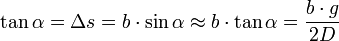
Man beobachtet also ein Interferenzmuster, wenn die so genannte Kohärenzbedingung erfüllt ist.
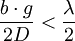
Um ein Interferenzmuster zu beobachten, darf die (inkohärente) Lichtquelle um so größer sein, je weiter sie vom Doppelspalt entfernt ist.
Betrachtet man die Sonne als Lichtquelle, so ist diese sehr groß, andererseits auch sehr weit weg. Welchen Spaltabstand muss der Doppelspalt haben, damit man Interferenz beobachten kann?
Daten:
- Durchmesser: 1,4⋅106 km
- mittlerer Abstand Erde – Sonne: 1,5⋅108 km
- Wellenlänge des Sonnenlichts: ≈ 500nm
und damit
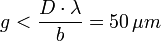
Direkt mit Sonnenlicht hätte Young den Versuch nicht mit einer Spielkarte als Doppelspalt durchführen können. Young hatte aber vor den Doppelspalt eine sehr feine Blende (das mit einer feinen Nadel in das Papier gestochene Loch), also müssen wir diese als Lichtquelle betrachten.
Wie weit musste der Doppelspalt mindestens vom Fenster entfernt stehen, dass Young Interferenz beobachten konnte?
Daten:
- Durchmesser des Lochs b: 1mm
- Spaltabstand g: 0,85mm
- Wellenlänge des Sonnenlichts: ≈ 500nm
und damit