Funktionsweise der optischen Pinzette

Im Folgenden wird erläutert, wie man mit einem fokussierten Laserstrahl ein Teilchen festhalten kann, oder anders ausgedrückt, wie man eine dreidimensionale optische Falle erzeugen kann.
 
Um ein Objekt an einer Stelle festzuhalten, muss es eine rückstellende Kraft erfahren, sobald es diese Stelle verlässt.
Bei einer optischen Falle wird das Teilchen im Laserfokus festgehalten, die rückstellende Kraft wird vom Laserstrahl ausgeübt.

Wie kann Licht eine Kraft auf ein Teilchen ausüben?

Grundvoraussetzung für das Einfangen eines Objektes ist, dass dieses für das verwendete Laserlicht durchsichtig ist, d.h. dass zumindest ein Teil des Lichts transmittiert werden kann.

Folgende Animation zeigt, was mit einem Laserstrahl passiert, der auf ein solches Objekt – in unserem Fall Kügelchen aus Polystyrol – fällt.

Ein Teil des Strahls wird reflektiert, der andere transmittiert.
Der reflektierte Strahl wird zur Vereinfachung nicht betrachtet.

Der uns interessierende Strahl wird jeweils an den Grenzflächen gebrochen, d.h. er ändert seine Richtung.
Das Entscheidende ist nun, dass Licht neben Energie auch Impuls trägt, dieser ändert sich offensichtlich, da das Licht ja seine Richtung ändert.
Der so übertragene Impuls muss nach dem Impulserhaltungssatz von dem Kügelchen stammen, mit anderen Worten: Zwischen Strahl und Kügelchen wirkt eine Kraft.
Intuitiv erwartet man, dass das Kügelchen vom Strahl weggestoßen wird, bei einer optischen Falle soll das Teilchen aber immer wieder in den Laserfokus zurückgezogen werden.

Wie kann das funktionieren?

Für eine optische Falle wird ein fokussierter Laserstrahl mit einer bestimmten Art von Intensitätsprofil benötigt, beispielweise eignet sich ein gaußsches Intensitätsprofil. Entscheidend ist, dass das Profil eine Stelle maximaler Intensität aufweist.

Betrachten wir zunächst einen unfokussierten Laserstrahl mit Gaußprofil:

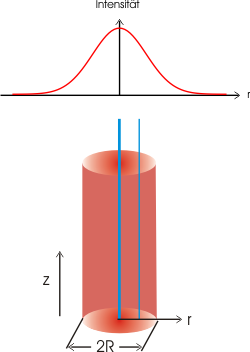
Der Laserstrahl hat einen bestimmten Durchmesser R, entlang dieses Radius ändert sich die Intensität, in der Mitte des Strahls ist sie am größten, nach außen hin fällt sie ab.
Im Folgenden wird der Laserstrahl, der einen endlichen Radius R aufweist, als ein Bündel von infinitesimalen Teilstrahlen betrachtet.
Beispielweise sagt man in diesem Sinn, dass ein (Teil-)Strahl aus der Mitte des Strahlbündels eine größere Intensität aufweist als ein Teilstrahl von weiter außen.
In der oben stehenden Graphik wurden als Beispiel zwei dieser Teilstrahlen durch blaue Linien stilisiert, ihre unterschiedlichen Dicken spiegeln die unterschiedliche Intensitäten wieder.
Der Laserstrahl ergibt sich als Summe aller dieser Teilstrahlen, vereinfachend werden wir jedoch im Folgenden immer nur zwei Strahlen betrachten, welche spiegelbildlich symmetrisch um die Strahlachse angeordnet sind.
Erkenntnisse, die mit diesen zwei Teilstrahlen gewonnen werden, können qualitativ auf den gesamten Laserstrahl übertragen werden.

Wir werden zunächst untersuchen, was passiert, wenn ein unfokussierter Laserstrahl auf eine Polystyrolkugel trifft, dabei werden wir zwei Fälle unterscheiden:

1. der Mittelpunkt der Kugel befindet sich auf der Strahlachse
2. der Mittelpunkt der Kugel befindet sich nicht auf der Strahlachse

Anschließend werden wir betrachten, was sich ändert, wenn wir den Laserstrahl fokussieren.

1a) unfokussierter Laserstrahl, Teilchen befindet sich im Strahlmittelpunkt

Betrachten wir nun den Verlauf zweier – wie oben erläutert – symmetrisch angeordneter Teilstrahlen, nennen wir sie s und t.

Die Strahlen haben die gleiche Intensität und Richtung (da sie beide den gleichen radialen Abstand zum Intensitätsmaximum haben), und damit tragen sie den gleichen Impuls.
Die Impulse der Strahlen sind in folgender Graphik für einige Stellen explizit als (blau und grün eingezeichnete) Pfeile dargestellt.
Dabei gibt die Pfeilrichtung die Richtung und die Länge des Pfeils den Betrag des Impulses wieder.

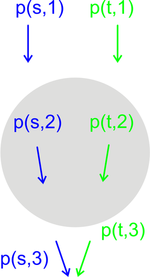
Dabei bedeutet zum Beispiel "p(s,1)": Der so beschriftete Pfeil stellt den Impuls des Strahles s an der Stelle 1 dar.
Man erkennt deutlich, dass sich der Betrag des Impulses, also die Länge der Pfeile, sich nicht ändert, sehr wohl aber die Richtung.
Nun werden die Pfeile vor Eintritt (Stelle 1) und nach Austritt (Stelle 3) aneinander gelegt, um so herauszufinden, wie sich der Impuls geändert hat.
Die Änderung des Impulses wird jeweils als orangefarbener Pfeil dargestellt.
(Alle Pfeile wurden der Übersichtlichkeit halber um den gleichen Faktor vergrößert)

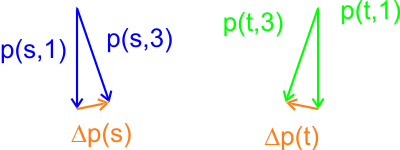
Nun legen wir die beiden orange-farbenen Pfeile aneinander, um so die Netto-Impulsänderung (als violetter Pfeil dargestellt) der beiden Strahlen herauszubekommen, diese können wir – wie oben erläutert – qualitativ auf das gesamte Strahlbündel – also den Laserstrahl – übertragen (wieder wurden die Pfeile der Übersichtlichkeit halber um den gleichen Faktor vergrößert)

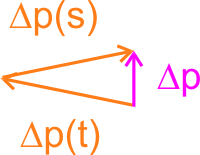
Man erkennt, dass der gesamte Laserstrahl eine Impulsänderung nach oben erfährt, nach dem Impulserhaltungssatz muss die Kugel also eine Impulsänderung nach unten erfahren, d.h. sie wird, wie wir intuitiv erwartet haben – vom Strahl nach unten weggedrückt.
Radial erhält man keine Impulsänderung, das ist gut, denn die Kugel soll ja im Strahlmittelpunkt bleiben.

Wie stellt sich die Situation jedoch dar, wenn sich die Kugel außerhalb des Strahlmittelpunkts befindet?

1b) unfokussierter Laserstrahl, Teilchen befindet sich außerhalb des Strahlmittelpunkts

Wir werden im Folgenden die gleiche Untersuchung wie in 1a) durchführen, diesmal werden die Pfeile der Übersichtlichkeit halber nicht beschriftet, da wir ja schon wissen, wann sie wie aneinander gelegt werden.

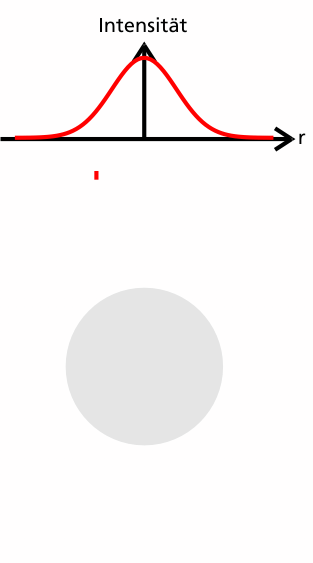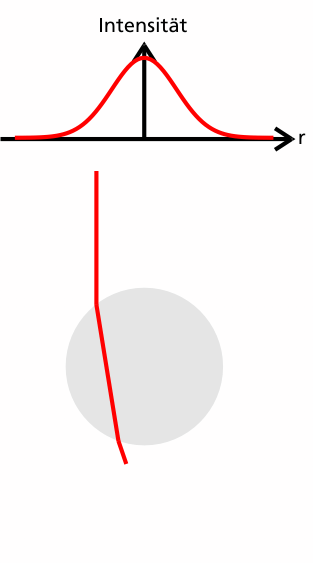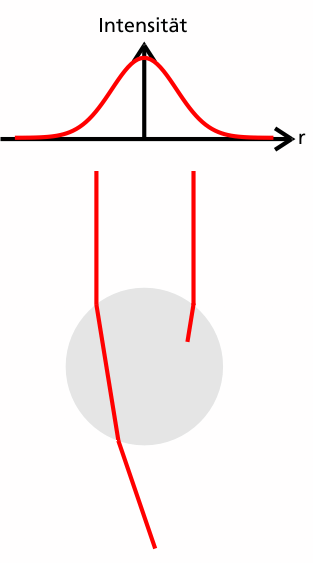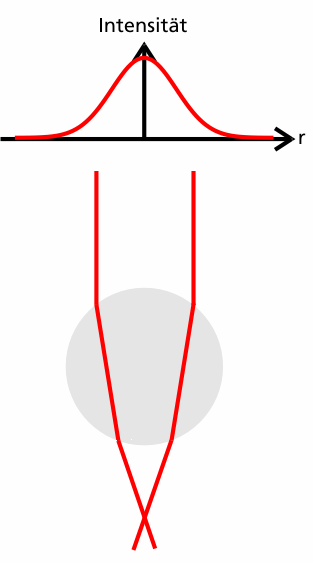
Die Kugel befindet sich nun also außerhalb des Strahlmittelpunkts, wieder wird der Verlauf zweier Teilstrahlen betrachtet.

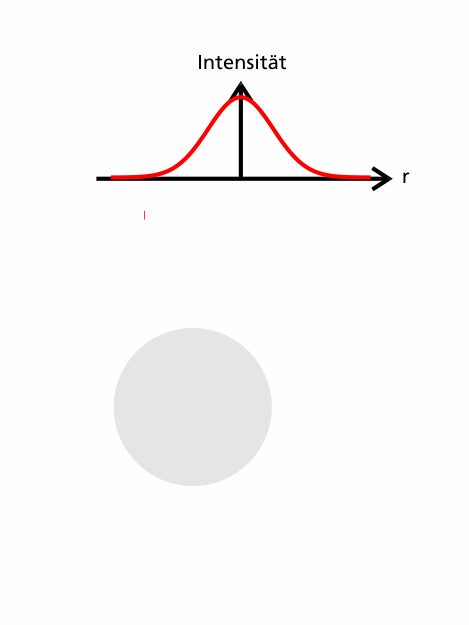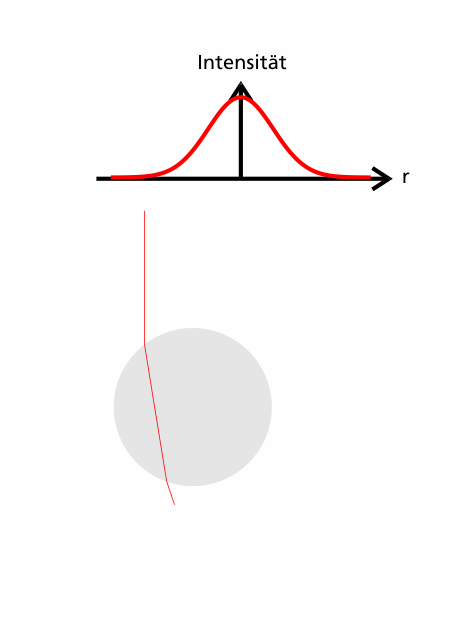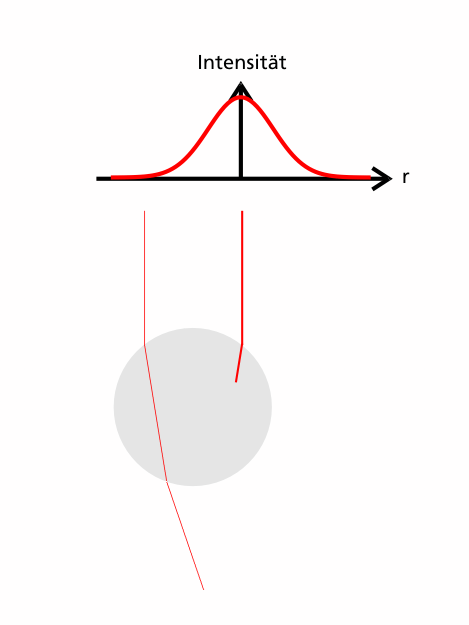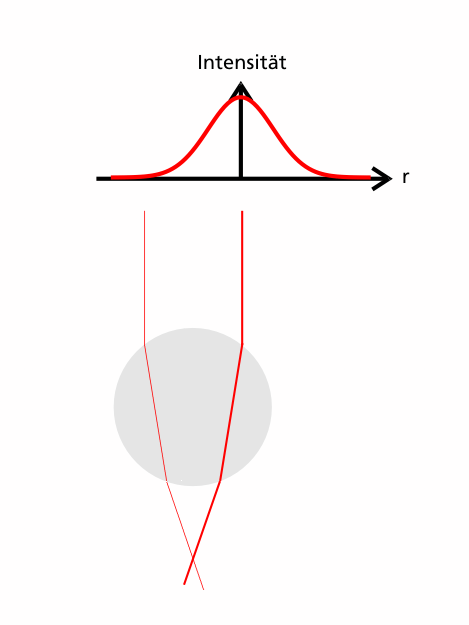
Diesmal haben nicht beide Teilstrahlen dieselbe Intensität, damit tragen sie auch nicht mehr den gleichen Impuls, wie an folgender Graphik verdeutlicht ist.

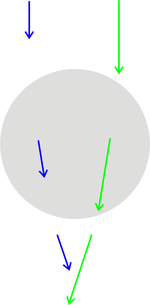
Damit erfahren die beiden Strahlen die folgend dargestellte Impulsänderung

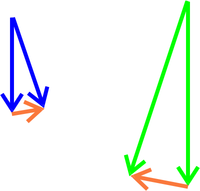
Die beiden Strahlen erfahren also eine – auch vom Betrag her – unterschiedliche Impulsänderung, somit erhalten wir für den gesamten Laserstrahl:

Der Laserstrahl erfährt also eine Impulsänderung nach links oben und damit erfährt die Kugel eine Impulsänderung nach rechts unten, sie wird also zurück zum Strahlmittelpunkt – zur Stelle der höchsten Intensität – gezogen.

Damit haben wir eine ideale zweidimensionale Falle erhalten, allerdings wird die Kugel immer noch nach unter weggedrückt, d.h. wir können sie nicht an einer Stelle halten.

Untersuchen wir nun, was passiert, wenn der Laserstrahl stark fokussiert wird, d.h. die Teilstrahlen nicht mehr parallel verlaufen. Betrachten wir den Fall, dass sich das Teilchen zwar im Strahlmittelpunkt befindet, aber unterhalb des Laserfokus.

2. fokussierter Laserstrahl, Teilchen befindet sich im Strahlmittelpunkt aber unterhalb des Laserfokus

Die folgende Animation zeigt zwei Teilstrahlen eines fokussierten Lasers, der Kugelmittelpunkt befindet sich unterhalb des Laserfokus.

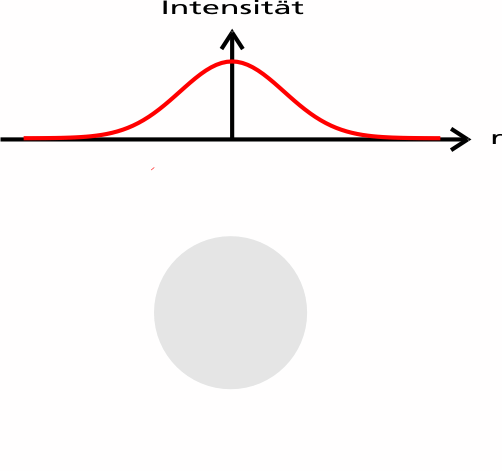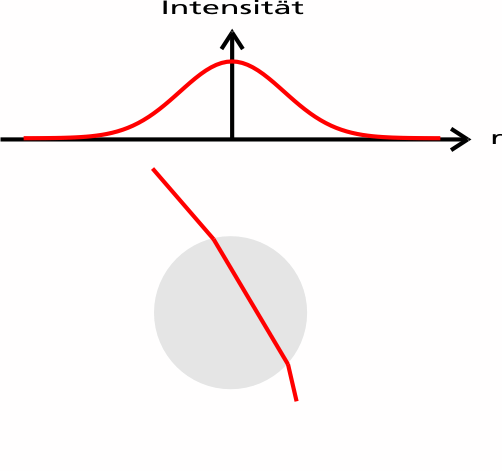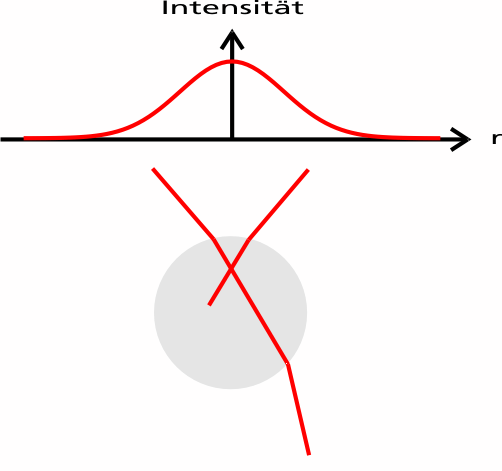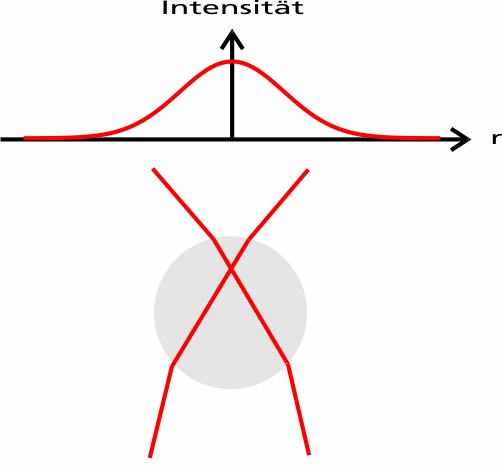
Da sich die Kugel im Strahlmittelpunkt befindet, haben beide Teilstrahlen die gleiche Intensität und tragen damit betragsmäßig den gleichen Impuls, allerdings ist die Richtung der beiden Impulse unterschiedlich, da der Strahl fokussiert ist.

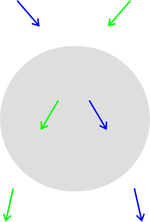
Betrachten wir wieder die Impulsänderung der beiden Teilstrahlen.

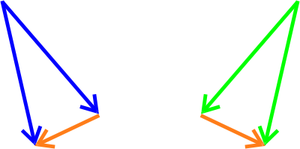
Und für den gesamten Laserstrahl

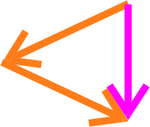
Der Laserstrahl erfährt eine Impulsänderung nach unten, die Kugel erfährt demnach eine Impulsänderung nach oben, d.h. sie wird zum Laserfokus hin gezogen.
Die Kugel bewegt sich also entgegen der Strahlrichtung – intuitiv hätten wir das Gegenteil erwartet!

Es lässt sich analog zeigen, dass die Kugel nach unten in den Laserfokus gezogen wird, wenn sie sich überhalb desselben befindet.

Damit haben wir mit einem einzigen Laserstrahl eine ideale dreidimensionale Falle erzeugt, fassen wir also noch einmal zusammen, was für eine optische Falle entscheidend ist!

Zusammenfassung

Um ein Objekt in einer dreidimensionalen optischen Falle zu fangen, benötigen wir einen stark fokussierten Laser mit einem geeigneten Intensitätsprofil, im einfachsten Fall gaußförmig.
Das Objekt wird immer in Richtung des Ortes der größten Intensität gezogen, also

• aufgrund des Intensitätsprofils (bei einem gaußförmigen)) radial in die Mitte des Laserstrahls  
• aufgrund der Fokussierung vertikal in Richtung des Laserfokus

Sobald sich das Teilchen aus dem Laserfokus bewegt, erfährt es eine rückstellende Kraft in Richtung des Laserfokus.