Zeigerdiagramme sind nützliche Werkzeuge in der Schwingungslehre. Auch im Bezug auf die Erklärung der Interferenzmuster bei Mehrfachspalten sind sie hilfreich, da mit ihnen die Phasenbeziehungen zwischen zwei Wellen veranschaulicht werden kann.

Die folgende Animation zeigt, dass sich eine sinusförmige Schwingung (zum Beispiel die eines Körpers an einem Federpendel) als Projektion einer Kreisbewegung darstellen lässt.

Die Funktionsgleichung der Schwingung sei

A(t) = Â⋅ sin(ωt)

Hier noch mal ein Bild der obigen Animation herausgegriffen:

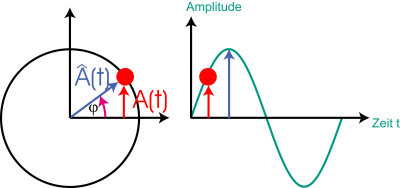
man erkennt dabei im Zeigerdiagramm folgendes:

• der Zeiger (blau) hat gerade die Länge Â, was der maximalen Amplitude entspricht.
• der Zeiger dreht sich entgegen dem Uhrzeigersinn mit der Winkelgeschwindigkeit ω
• der Winkel zwischen Zeiger und der horizontalen Achse ist durch φ = ωt gegeben.
• Die Länge der Vertikalen (grün eingezeichnet) ist dann gerade der Funktionswert, also die Amplitude zu einer gegebenen Zeit.
  

Die Phase φ kann ich Grad oder im Bogenmaß angegeben werden, also z.B.

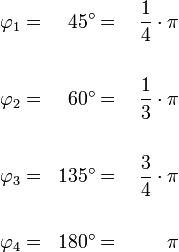
Auch bei der Betrachtung von Wellen sind Zeigerdigramme hilfreich.

Betrachten wir im Folgenden nun Licht als elektromagnetische Welle.
Greift man einen festen Ort der Welle heraus, so schwingt der Vektor des elektrischen Feldes, wie folgende Animation einer sich nach rechts ausbreitenden Welle zeigt.

Betrachtet man nun zwei sich überlagernde Wellen gleicher Frequenz sowie konstanter Phase und Amplitude, so kann die Amplitude der resultierenden Welle mit Hilfe des Zeigerdiagramms leicht berechnet werden, wie folgende zwei Beispiele zeigen:

Beispiel 1

Besteht zwischen den beiden Wellen (in blau und rot eingezeichnet) keine Phasendifferenz, so können die Amplituden (resultierende Welle in grün eingezeichnet) einfach addiert werden:

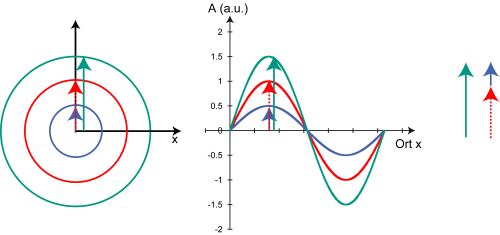
Beispiel 2

Besteht zwischen zwei sich überlagernden Wellen (in blau und rot eingezeichnet)  eine Phasendifferenz von Δφ kann die Amplitude der resultierenden Welle (in grün eingezeichnet)  leicht im Zeigerbild ermittelt werden:

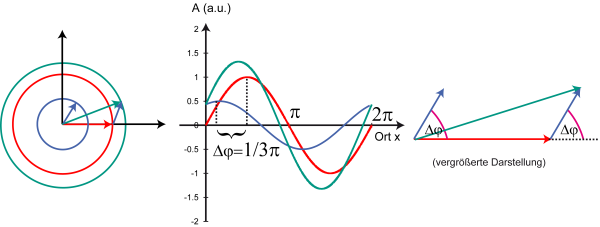
Die resultierende Amplitude erhält man also durch Vektoraddition der Zeiger.

Zusammenhang von Phasendifferenz und Gangunterschied

Im Bezug auf die Erklärung von Interferenzmustern ist der Zusammenhang von Phasendifferenz  und Gangunterschied interessant.

Entspricht der Gangunterschied gerade einer Wellenlänge, so ist die Phasendifferenz 2π. Entspricht der Gangunterschied einer halben Wellenlänge, beträgt die Phasendifferenz  π.
Allgemein gilt also folgender Zusammenhang zwischen Phasendifferenz  und Gangunterschied:

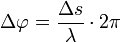
Zurück zum Dreifachspalt.